Summary
Merkle Tree는 블록체인에서 트랜잭션의 무결성을 검증하고 요약하는 해시 트리 구조입니다. 이는 트랜잭션 데이터를 효율적으로 검증하고 보관하는 데 사용됩니다.
Description
Merkle Tree는 블록체인 기술에서 중요한 데이터 구조로, 트랜잭션의 무결성을 검증하고 요약하는 역할을 합니다. Merkle Tree는 다음과 같은 구조로 이루어져 있습니다:
- 리프 노드 (Leaf Node): Merkle Tree의 가장 하단에 위치하며, 각 리프 노드는 개별 트랜잭션의 해시 값을 저장합니다.
- 브랜치 노드 (Branch Node): 리프 노드 위에 위치하며, 각 브랜치 노드는 하위 노드들의 해시 값을 결합하여 저장합니다.
- 루트 노드 (Root Node): Merkle Tree의 최상단에 위치하며, 전체 트리의 최종 해시 값인 머클 루트(Merkle Root)를 나타냅니다.
Bitcoin 블록체인에서는 Merkle Root를 계산하기 위해 트랜잭션의 해시 값을 두 번 SHA-256으로 해싱하는데, 이를 기호 D로 나타낸다고 가정합시다. 각 트랜잭션의 해시 값은 H = D(트랜잭션)으로 계산됩니다. Merkle Tree는 홀수 개의 트랜잭션이 있을 경우 마지막 트랜잭션을 중복하여 짝수 개로 맞춘 후 계산합니다.
참고로, Python을 사용하여 구현할 때에는 Big-endian 방식의 계산과 Bitcoin 노드에서의 Little-endian 동작 방식의 차이를 고려하여 [::-1] reverse slicing을 진행해야 합니다.
예를 들어, 7개의 트랜잭션(T1, T2, T3, T4, T5, T6, T7)이 주어졌을 때 Merkle Root를 계산하는 과정은 다음과 같습니다:
-
각 트랜잭션의 해시 값을 계산합니다:
- H1 = D(T1)
- H2 = D(T2)
- H3 = D(T3)
- H4 = D(T4)
- H5 = D(T5)
- H6 = D(T6)
- H7 = D(T7)
-
리프 노드의 해시 값을 결합하여 브랜치 노드를 계산합니다:
- H12 = D(H1 + H2)
- H34 = D(H3 + H4)
- H56 = D(H5 + H6)
- H77 = D(H7 + H7) # 홀수 개의 트랜잭션이므로 H7을 중복 사용
-
브랜치 노드의 해시 값을 결합하여 상위 브랜치 노드를 계산합니다:
- H1234 = D(H12 + H34)
- H5677 = D(H56 + H77)
-
최종적으로 Merkle Root를 계산합니다:
- Merkle Root = D(H1234 + H5677)
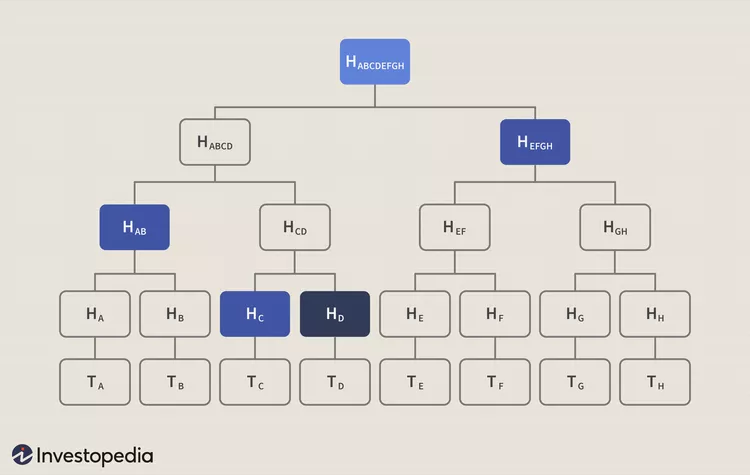
블록 H_D가 트리에 포함되어 있는지 검증하기 위해, 3개 블록 H_C, H_AB, H_EFGH 값만 가져오면 된다.
References
- # 4 - 머클트리(Merkle Tree) 및 머클루트(Merkle Root)에 관한 정의
- 머클트리(Merkle Tree)란?
- 1-2. 머클트리(Merkle Tree)란?
- Merkle Tree in Blockchain: What It Is and How It Works